Dedicated DEFFEM simulation package

Highlights

  • Computational system dedicated for cooperation with Gleeble 3800 physical simulator
  • In-house, highly-adaptive numerical code
  • No external (commercial) modelling software necessary
  • Keywords modelling approach
  • Advanced Post-processor including 3D stereoscopic visualization and capabilities of GPU processors NVidia graphics cards
  • Capabilities: hot forging, solidification, thermal analysis, fluid simulation, resistance heating, grain-growth modelling
  • 3D rigid-plastic FEM-based thermo-mechanical solver, 3D thermal FEM-based solver, Monte-Carlo 3D based microstructure model, 3D fluid with thermal capabilities SPH-based solver

Scientific background

The research, developmental and scientific work carried out since 2012 as part of project financed by National Science Centre, resulted in the development of a modelling concept integrating the physical and computer simulation areas, whilst providing full or partial exchange of information between those areas. The proposed concept utilizes the capabilities of the thermo-mechanical simulators in the high-temperature materials processing. The other necessary and unique component is the continuously developed original simulation package DEFFEM. The whole modelling approach is complemented by the utilization of modern testing and measurement instruments to verify the implemented solutions or to obtain additional information that cannot be obtained by traditional methods [1]. The coupling and exchange of information between the areas of physical and computer simulations allows, among others, the necessary data for the needs of numerical simulations (stress-strain curves, characteristics of changes in the current intensity as a function of time, local temperature changes within the sample volume, local cooling rates, macro- and microstructure etc.) to be identified. At the same time, the application of computer simulations using the dedicated simulation system DEFFEM allows the obtained physical simulation findings to be interpreted.
The general outline of the developed concept is presented in Fig. 1.

 

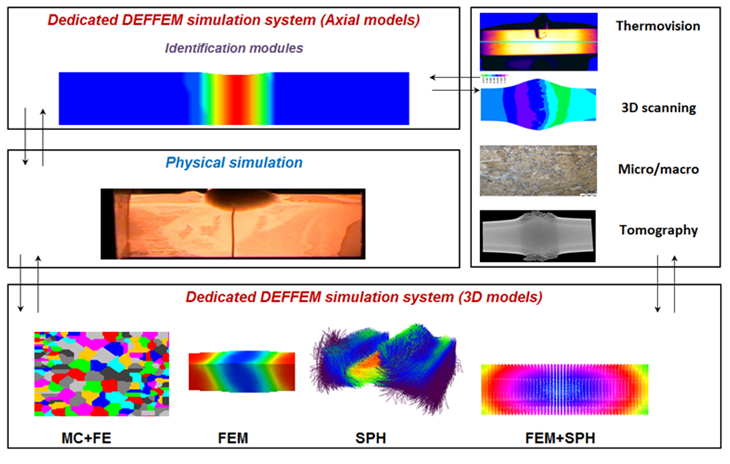Fig. 1. Integrated modelling concept as the basis of the scientific workshop focused on high-temperature processes

Main computational capabilities of the DEFFEM package

The DEFFEM simulation package is being developed in pursuance with the design philosophy ONEDES (ONEDECisionSoftware) [1,2]. It is based upon the assumption of numerical implementation of a set of independent modules comprising the DEFFEM package, fully integrated with the Gleeble 3800 simulator, not requiring a support in commercial solutions. The current version of the DEFFEM package offers very broad capabilities regarding the adaptation of numerical codes to the specified tasks. It concerns largely a change in the boundary conditions, importing of a mesh defining a new computing area, or stabilizing the numerical solution.

extra-high temperature deformation resistance heating
Fig. 2. Strain distribution, Z-component of tensor (deformation at a nominal temperature of 1400°C, S355 grade steel) Fig. 3. Temperature distribution after 10 seconds of resistance heating in the Gleeble 3800 simulator system (surface temperature 198.286°C,  S355 grade steel)

 

solidification

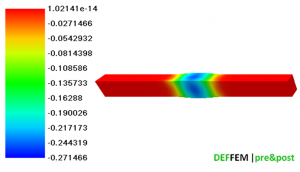
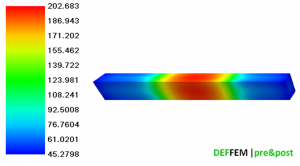
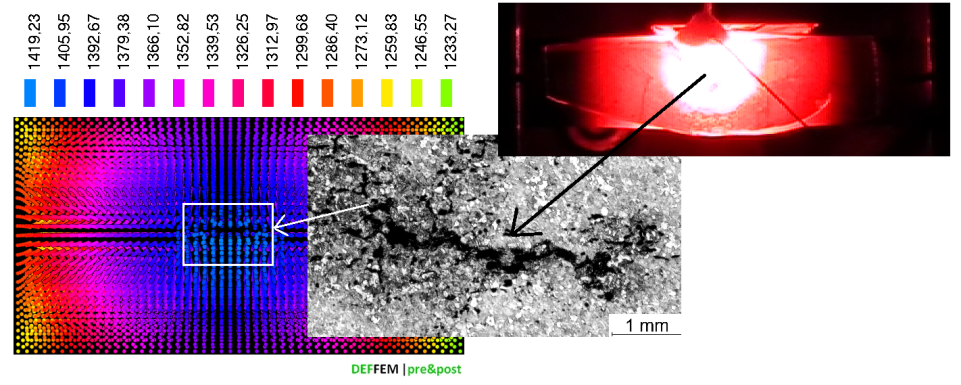
Fig.4. Temperature distribution on a sample cross-section after the completed solidification process with visible defects within the sample volume, and an example of sample microstructure after the remelting process  (C45 steel grade)

 

fluid-flow grain-growth
Fig. 5. The velocity field for a selected fluid flow stages (A-D) in the interaction with the object Fig. 6. Example macrostructure for a selected heating/melting/cooling stages

Contact person:

Marcin Hojny, Ph.D., Eng., mhojny(at)metal.agh.edu.pl

Key publications:

[1] M. Hojny, Modeling steel deformation in the semi-solid state, Springer International Publishing, 2018
[2] M. Hojny, Projektowanie dedykowanych systemów symulacji odkształcania stali w stanie półciekłym, Wzorek Publishing, 2014

Connected projects:

The project has been supported by the Polish National Science Centre, Decision number: DEC 2011/03/D/ST8/04041 (2012-2018)